Ausgabe 2 2023 / 2/2023

Deine Finger sind kleine Mathe-Genies!

• von Alexej Michirev, Maša Iskra & Laura Voigt

Hast du schon einmal deine Finger zum Rechnen benutzt? Hat jemand dann gesagt, dass du doch schon groß bist und ohne deine Finger rechnen solltest? Höre nicht auf sie! Längst weiß man, dass deine Finger wertvolle Helfer beim Rechnen sein können, zum Beispiel, wenn du Zahlen „im Kopf“ halten musst. Studien zeigen: Je geschickter Kinder mit ihren Fingern sind, desto besser sind ihre Mathekenntnisse. In diesem Artikel zeigen wir dir, warum und wie du deine Finger im Matheunterricht nutzen kannst.

Dir ist sicher schonmal aufgefallen, für was du alles im Alltag deine Finger nutzen kannst, oder? Wenn du beim Bäcker bist, zeigst du wahrscheinlich auf ein Gebäck oder einen ganzen Kuchen, von dem du etwas haben möchtest. Eventuell hältst du dann drei Finger hoch, um zu zeigen, wie viele Kuchenstücke du möchtest. Vielleicht benutzt du sie manchmal auch bei komplizierteren Matheaufgaben, um die Aufgabe in kleineren Schritten zu lösen. Und das ist auch gut so! Denn das Praktische an deinen Fingern ist, dass du sie immer dabeihast und nicht auf andere Hilfsmittel angewiesen bist, die du auch mal vergessen könntest.

Wie du deine Finger zu Mathe-Genies entwickelst

In deinem Alter entwickelst du dich sehr schnell. Deine Entwicklung in Gehirn und Körper sind stark miteinander verbunden. Du lernst jeden Tag ständig neue Dinge dazu: Du wirst besser und schneller im Zählen und Rechnen. Dein Körper wird stärker und schneller: Deine Finger werden beweglicher und feinfühliger. In der Fachsprache nennt man die Beweglichkeit deiner Finger Feinmotorik und die Feinfühligkeit deiner Finger nennt man Fingergnosie.

Studien mit Kindern haben gezeigt, dass je besser die Kinder in Feinmotorik und Fingergnosie sind, desto besser sind sie auch in Zählen, Rechnen und im Matheunterricht allgemein (Barrocas et al., 2020*). Das liegt daran, dass Finger dazu beitragen, ein besseres Verständnis von Zahlen zu entwickeln. Angefangen hat es, als du noch jünger warst und mit deinem Finger auf etwas gezeigt hast, wenn du etwas gerne haben wolltest (ein Stück vom Kuchen). Da schon hast du verstanden, dass dieser eine Finger für dieses eine Stück Kuchen steht. Somit hast du eine Einheit (das Stück Kuchen) und einen deiner Finger miteinander verknüpft (Alibali & Dirusso, 1999; Butterworth, 1999). Einige Jahre später hast du deine Finger auch fürs Zählen und dann fürs Rechnen benutzt und dein Zahlenverständnis hat sich mit verbessert. Auch wenn du jetzt ohne deine Finger bis zehn und weiter zählen kannst, hängen dein Zahlenverständnis und deine Finger weiterhin fest zusammen. Du kannst dein Zahlenverständnis weiterhin trainieren, indem du deine Finger trainierst.

Feinmotorik ist ein grundlegender Bestandteil deiner Entwicklung und umfasst die Beweglichkeit deiner Finger. Je besser deine Feinmotorik in den Fingern, desto geschickter bist du zum Beispiel im Schuhe zubinden, Tippen auf dem Handy, und im Spielen von Musikinstrumenten. Diese Aufgaben haben eins gemeinsam: sie erfordern feinfühlige Beweglichkeit deiner Finger. Das Ausführen dieser Aufgaben verbessert wiederrum deine Feinmotorik. Auch in Aufgaben, in denen dein Zahlenverständnis erforderlich ist, wie zum Beispiel Rechnen, wirst du erfolgreicher sein, je besser, schneller und geschickter du deine Finger bewegen kannst.

Eine Ergänzung zur Feinmotorik stellt die Fingergnosie dar. Fingergnosie ist die Fähigkeit, die einzelnen Finger zu fühlen und voneinander unterscheiden zu können, ohne dabei auf die Finger zu schauen (Gracia-Bafalluy & Noël, 2008). Leg deine Hände auf den Tisch und bitte eine Person, dir mit etwas Weichem (zum Beispiel einer Feder) ganz sanft über die einzelnen Finger zu streichen. Konntest du problemlos jeden einzelnen Finger erkennen? Falls ja, prima! Falls du aber weiterüben möchtest, findest du am Ende des Artikels eine passende Übung (siehe Abbildung 1 Klavierübung).

Zusammengefasst: Feinmotorik und Fingergnosie, also die Beweglichkeit und Feinfühligkeit deiner Finger, sind wichtige Fähigkeiten für deinen Alltag und können dir dabei helfen, dein Zahlenverständnis zu verbessern. Wenn du sie also bewusst trainierst, wirst du noch besser werden. Das kann sich dann sehr positiv auf dein Lernen im und außerhalb des Matheunterrichtes auswirken. Denk daran, Übung macht den/die MeisterIn!

Warum das Dezimalsystem so herausfordernd ist und wie du dieses meistern kannst

Immer wieder stehst du vor neuen Herausforderungen in deinem Leben. Mathematische Herausforderungen sind da keine Ausnahmen. Vielleicht erinnerst du dich noch daran, als du an deinen Fingern gezählt hast und jemand gefragt hat, welche Zahl nach der 5 kommt? Warst du da verwundert? Denn bisher hattest du stets an einer Hand die Finger abgezählt, die jetzt nicht mehr ausgereicht haben.

Der Übergang in das 10er System fällt vielen Kindern am Anfang schwer. Wenn du mit Zahlen bis 100, 1000 oder noch höher rechnen möchtest, brauchst du das Dezimalsystem (auch genannt: Basis 10, Zehnerstopp oder Zehnerübergang). Es ist wichtig, dass du den Umgang mit diesen Zahlen beherrschst, um zum Beispiel beim Sport die Punkte mitzuzählen, deinen Einkauf zu berechnen oder die Uhr zu lesen. Das Dezimalsystem ist also der Grundstein der Mathematik im Alltag und basiert auf der Zahl 10. Bis heute hast du einzelne Zahlen sehr gut lernen können, zum Beispiel die Zahl 3 und die Zahl 5. Im Dezimalsystem haben die beiden Zahlen jedoch eine ganz andere Bedeutung, wenn sie zusammen für eine einzige große Zahl stehen. Je nach Kombination können sie entweder für eine „35“ oder eine „53“ stehen. Das nenn man auch den „Stellenwert“ einer Zahl. Auch hier kannst du deine Hände und Finger weiterhin benutzen, um dir Zahlen bildlich darzustellen und den Stellenwert zu verändern. Bei der Zahl „35“, könntest du 3 Finger der linken Hand ausstrecken, um die 3 darzustellen, und 5 Finger der rechten Hand, um die 5 darzustellen. Mit solchen Übungen lernst du schnell den Stellenwert der Zahlen. Bei einer „35“ stehen die 3 Finger für die ganze „30“ und hat somit einen größeren Stellenwert (die Zahl 3 steht links innerhalb der „35“). Die Zahl 5 steht rechts („35“) und hat somit den kleineren Stellenwert. Wenn du jedoch anstelle der „35“ die „53“ hast, dreht sich der Stellenwert um. In der Zahl „53“ hat die Zahl 5 einen größeren Stellenwert und die Zahl 3 einen kleinen Stellenwert. Für die Zahl „53“ würdest du die fünf Finger der linken Hand austrecken um die 5 darzustellen und drei Finger der rechten Hand ausstrecken, um die 3 darzustellen. Hier würde die Zahl 5 für die ganze 50 stehen und somit den größeren Stellenwert haben (siehe Abbildung 2A und 2B).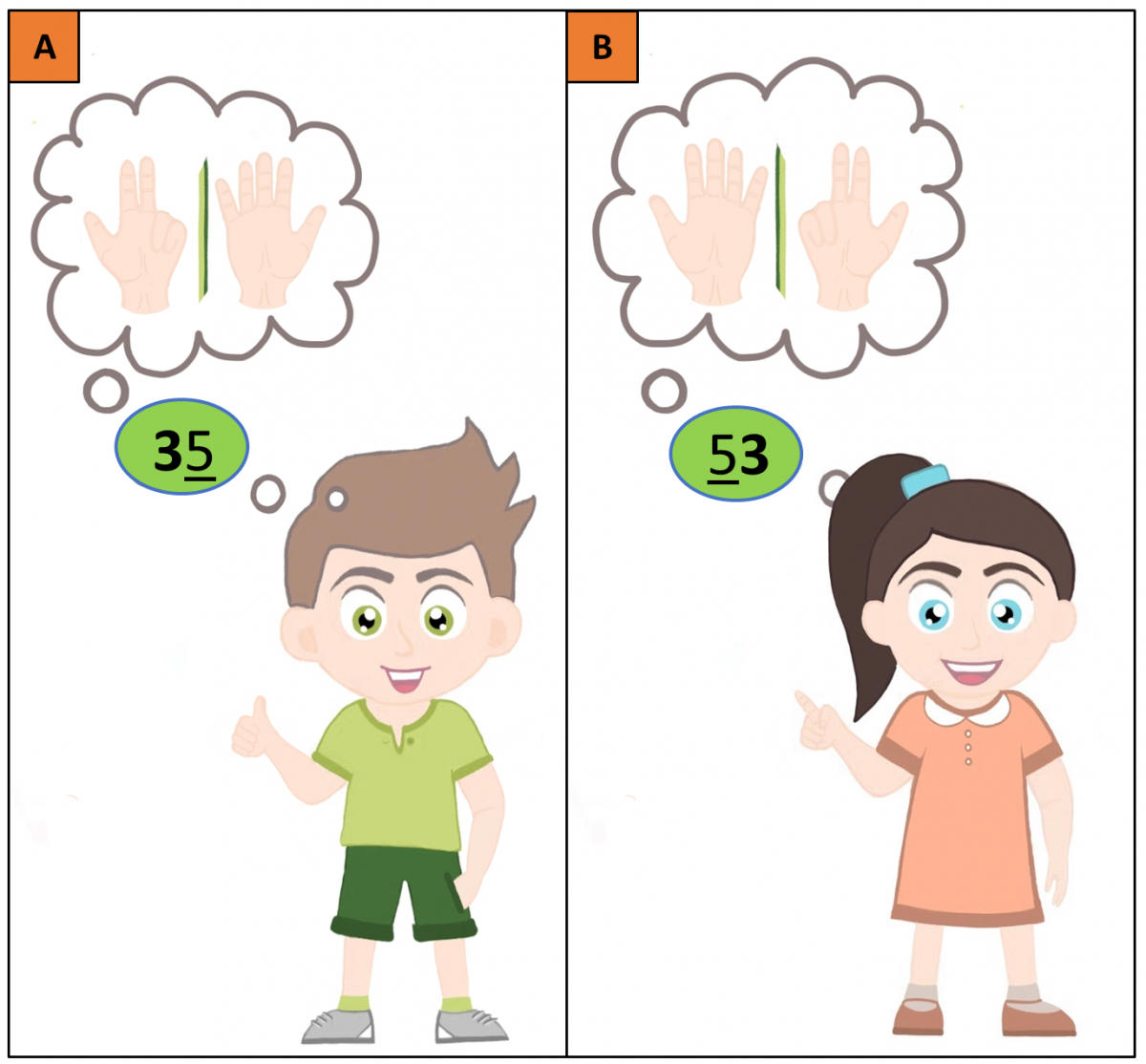
Bild 2: Übung: Stellenwert der Zahlen

Wenn du es auch für andere Zahlen versuchen möchtest, zum Beispiel eine „47“, musst du deine Strategie ein wenig anpassen. Halte zuerst 4 Finger hoch, die dann für die 40 stehen, weil die 4 links in der „47“ steht. Merke sie dir. Dann benutze wieder beide Hände und strecke 7 Finger aus, um die 7 an die 4 anzureihen („47“; siehe Abbildung 2B). Statt mit deinen Händen, kannst du das auch mit Gegenständen machen: Lege 4 Bauklötze (oder etwas Anderes) aufeinander und dann 7 weitere in einem anderen Stapel daneben. Zusammen formen die beiden Stapel dann eine 4 und eine 7, was insgesamt für 47 steht (siehe Abbildung 3A + 3B).

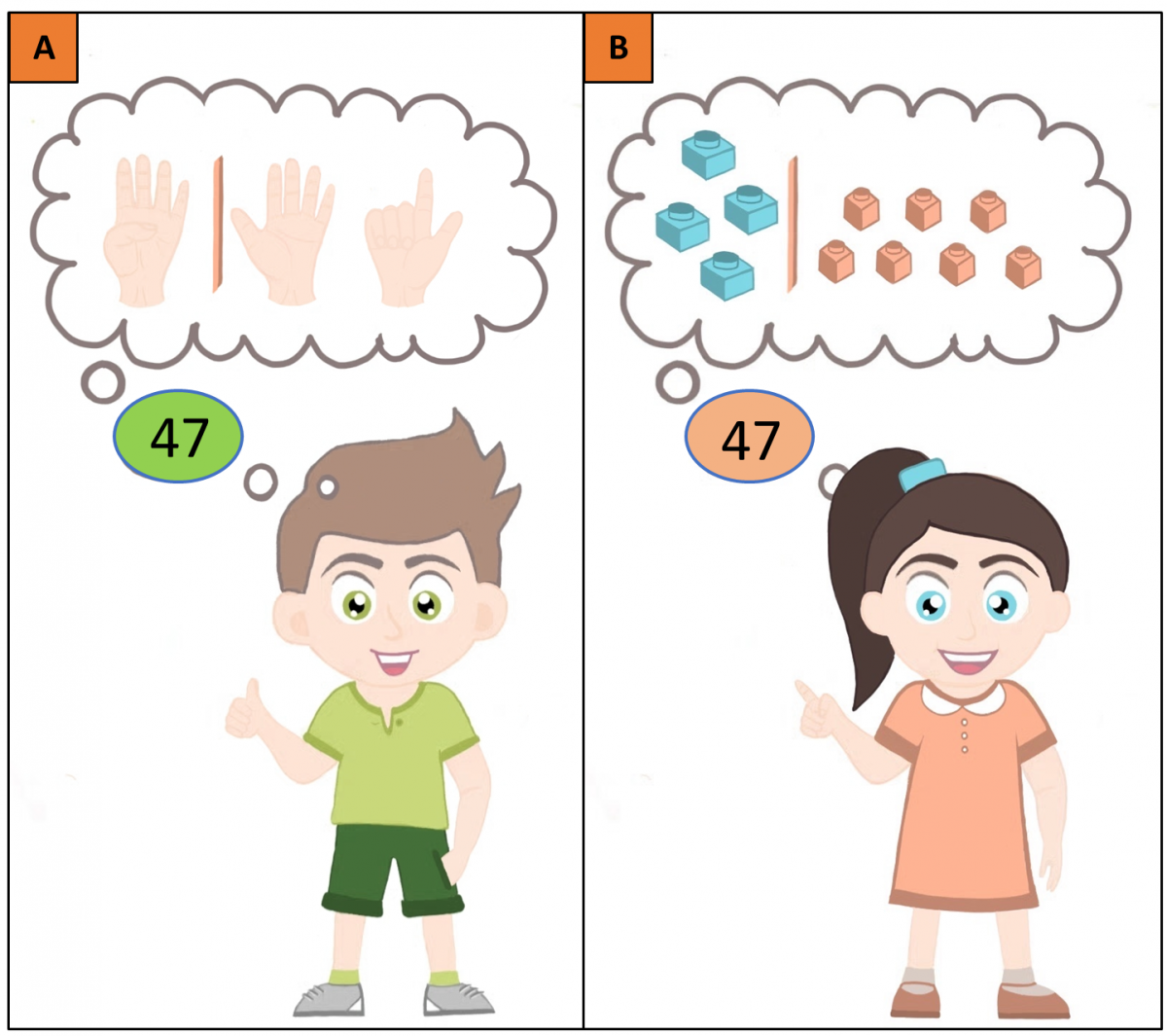Bild 3: Übung: Stellenwert der Zahlen – mit Fingern oder Gegenständen.

Am Ende dieses Artikels findest du eine weitere Übung, die dir zeigt, wie man größere Zahlen miteinander multipliziert. Schau dir dafür die Abbildung 4 an. Diese Übung ist fortgeschritten, daher empfehlen wir dir, in Ruhe und mit Hilfsmitteln (Stift und Papier) zu üben. Suche auch selbst noch nach anderen hilfreichen Tricks (zum Beispiel im Internet)! Wir möchten dich ermutigen, deine Finger so zum Zählen und Rechnen zu nutzen, wie es dir zum Lösen deiner Aufgaben hilft. Es gibt verschiedene Arten, seine Finger für Matheprobleme zu verwenden. Falls andere Menschen ihre Finger anders nutzen als du, bedeutet es nur, dass ihnen es so leichter fällt. Es heißt nicht, dass es besser oder schlechter ist. Solange du deine Finger zum Üben benutzt, entwickelst du auch deine Feinmotorik und Fingergnosie weiter (die Beweglichkeit und Feinfühligkeit deiner Finger). Wenn du Bauklötze oder ähnliches benutzt, verbesserst du die Fingergnosie, weil du Gegenstände anfasst und fühlst. Hier noch ein kleiner Tipp: Wenn du Gegenstände benutzt, dann versuche möglichst unterschiedliche Formen, Größen und Oberflächen zu verwenden (z. B. Bastelzeug). Das trainiert deine Finger und macht sie feinfühliger. Und das weißt du ja schon: je besser, schneller und geschickter du deine Finger bewegen kannst, desto erfolgreicher bist du im Schuhe zubinden, Tippen auf dem Handy, im Spielen von Musikinstrumenten und in der Mathematik. Deswegen sind deine Finger deine kleinen Helfer und Mathe-Genies!

Zusammenfassung

Manchmal hört man, dass man in Mathe erst richtig gut ist, wenn man jede Aufgabe im Kopf lösen kann. Wenn du schwierige Aufgaben zwar lösen kannst, aber dazu manchmal noch deine Finger verwendest, guckt man dich schief an. Vielleicht hast du bisher auch selbst gedacht, dass es ein Zeichen des Nichtkönnens ist, deine Finger beim Rechnen als Helfer zu nehmen. Wir versichern dir: das stimmt nicht! Zum richtigen Zeitpunkt wirst du deine Finger nicht mehr benutzen, denn das ist eine natürliche Entwicklung. Das solltest du jedoch nicht erzwingen. Bis es soweit ist, solltest du dich auf deine Finger verlassen und auch damit üben. Das wird dir im Alltag enorm helfen und kann deinen Lernerfolg außerhalb und innerhalb des Matheunterrichts erheblich verbessern. Wir möchten dich somit ermutigen, einen besonderen Wert auf deine Finger zu legen, denn sie sind deine eigenen Mathe-Genies!

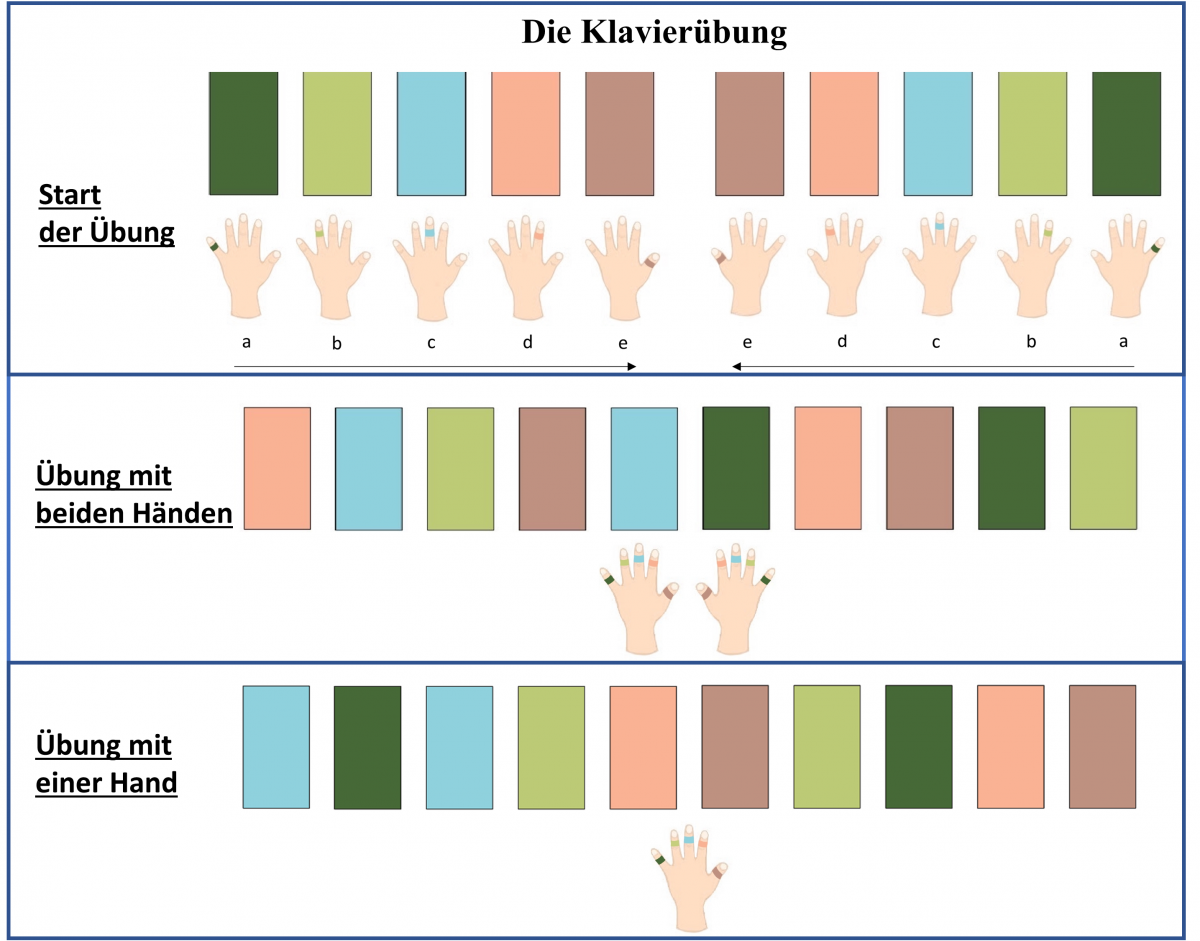
Anleitung "Die Klavierübung"

Bei dieser Übung geht es darum, das Feingefühl deiner Finger zu verbessern. Stell dir in dieser Übung vor, du würdest auf einem Klavier spielen. Beim Start der Übung brauchst du 10 bunte „Klaviertasten“ (z. B. Papierblätter), von denen jeweils 2 gleichfarbig sind. Du kannst beliebige Farben nutzen. Platziere die „Klaviertasten“ wie beim Start der Übung. Dann malst du deinen kleinen Finger der linken und rechten Hand dunkelgrün an (oder klebst einen kleinen, dunkelgrünen Zettel auf deinen Finger). Das ist dann Schritt „a“ im Bild. Tippe nun ganz leicht mit deinen kleinen Fingern nacheinander die dunkelgrünen „Klaviertasten“ an. Nach ein paar Versuchen malst du zusätzlich deine Ringfinger hellgrün (wie im Schritt „b“) und tippst nun mit deinen Ringfingern nacheinander die hellgrüne „Klaviertaste“ an. Wiederhole die Schritte für „c“, „d“, und „e“. Bei der Übung mit beiden Händen hast du den Start der Übung schon geschafft und hast all deine Finger angemalt. Lege nun deine „Klaviertasten“ in einer anderen und zufälligen Reihenfolge auf und versuche mit deinen farbigen Fingern die passende „Klaviertaste“ zu finden und sie anzutippen. Und so spielst du das „farbige Klavier“! (Gracia-Bafalluy & Noël, 2008).

Bild 1: Die Klavierübung

Anleitung "Fortgeschrittene Übung: Multiplikation"

Jede Multiplikation der Zahlen 6-10 ist mit diesem Trick möglich! Dies ist eine Übung für Fortgeschrittene. Nimm dir ruhig einen Stift und ein Blatt Papier zur Hand und schreibe die einzelnen Schritte mit. So ist es leichter, die Übung zu verstehen und zu üben

Zum Beispiel könntest du so 7 x 8 rechnen. Befolge dafür die folgenden Schritte:

1. Du kannst deinen Fingern an beiden Händen Zahlen zugewiesen. Mach es so wie im Bild 4B. Vielleicht ist es einfacher, die Zahlen direkt auf die Finger zu zeichnen.
2. Achte auf die blauen Zahlen im Beispiel 4B. Nun, nimm den Finger einer Hand, dem du die Zahl 7 zugewiesen hast, und einen Finger der anderen Hand, dem du die Zahl 8 zugewiesen hast.
3. Führe die beiden Finger zusammen, sodass sie sich berühren.
4. Zähle die beiden Finger, die sich berühren (2) und die Finger darunter (es sind insgesamt 3 Finger unterhalb der sich berührenden Fingern). Zusammen ergeben sie die Zahl 5. Das ist die Zahl, die links im Ergebnis stehen wird.
5. Achte auf die grünen Zahlen im Beispiel 4B. Multipliziere nun die Finger oberhalb der sich berührenden Finger. Das sind 3 auf der einen Hand und 2 auf der anderen Hand. Zusammen sind es dann 3 x 2, was eine 6 ergeben. Das ist die Zahl, die rechts im Ergebnis steht.
6. Zusammen ist dies die Lösung! 5 und 6 stehen für 56.  
7. 7 x 8 = 56

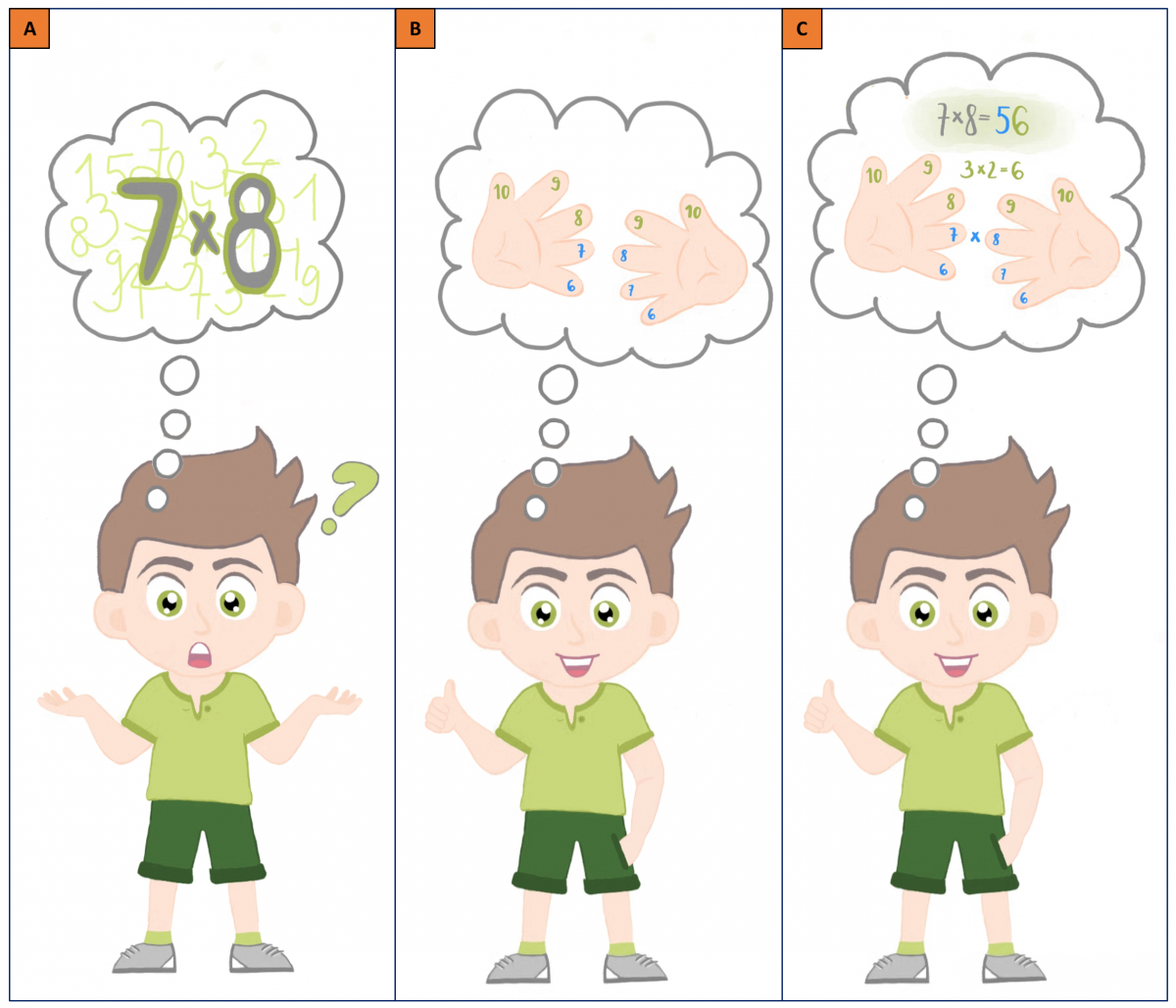Bild 4: Fortgeschrittene Übung: Multiplikation

 *In Klammern werden die AutorInnennamen angegeben, die zu diesem Thema schon geforscht haben, z. B. so: Butterworth, 1999. Das bedeutet, dass jemand namens Butterworth im Jahr 1999 dazu geforscht hat. Diese Vorarbeiten findet ihr ganz unten, am Ende des Artikels, ausgelistet.

Literaturverzeichnis

Alibali, M. W., & Dirusso, A. A. (1999). The function of gesture in learning to count: More than keeping track. Cognitive Development, 14(1), 37–56. https://doi.org/10.1016/S0885-2014(99)80017-3

Barrocas, R., Roesch, S., Gawrilow, C., & Moeller, K. (2020). Putting a finger on numerical development – Reviewing the contributions of kindergarten finger gnosis and fine motor skills to numerical abilities. Frontiers in Psychology,11. https://doi.org/10.3389/fpsyg.2020.01012

Butterworth, B. (1999). The mathematical brain. Macmillan.

Gracia-Bafalluy, M., & Noël, M. P. (2008). Does finger training increase young children’s numerical performance? Cortex, 44(4), 368–375. https://doi.org/10.1016/j.cortex.2007.08.020

Bildquellen:

Bild 1: Eigentum der Autor*innen

Bild 2: Eigentum der Autor*innen

Bild 3: Eigentum der Autor*innen

Bild 4: Eigentum der Autor*innen