Ausgabe 4 2015 / Kognitionspsychologie im Alltag. Teil 2: Lernen und Gedächtnis

Bitte drängeln, dann geht alles schön der Reihe nach – wie wir Reihenfolgen abspeichern und wiedergeben

• von Robert Gaschler & Nicolas W. Schuck

Wörter richtig tippen, Treppen steigen ohne zu stolpern, sprechen, musizieren, Protokolle abarbeiten,… – Reihenfolgen bestimmen unseren Alltag. Es fällt selten auf, dass die Präzision erstaunlich ist, mit der wir Sequenzen produzieren oder wahrnehmen können. Beispielsweise müssen die Sprechmuskeln in sehr kleinen zeitlichen Abständen und in korrekter Reihenfolge präzise Impulse bekommen –  damit ein gesprochenes Wort dabei herauskommt. Reihenfolge und Zeit, in der verschiedene Finger verschiedene Gitarrensaiten zupfen, bestimmen, welche Melodie zu hören ist. Eine präzise Sequenzierung von Muskelbewegungen ist aber schon allein dafür notwendig, sich die Schuhe richtig zu binden, um auf dem Weg zum Probenraum nicht zu stolpern.

Für gewöhnlich sind die Schnürsenkel gebunden, die Finger treffen die richtigen Saiten zur richtigen Zeit, wir sprechen munter drauf los und hören manchmal auch zu – wo ist also das Problem? Wissenschaft ist vielleicht oft dann besonders spannend, wenn sie herausarbeitet, dass vermeintlich Selbstverständliches eigentlich gar nicht selbstverständlich ist. Serielle Ordnung im Verhalten ist ein Problem – so der Titel des 1951iger Aufsatzes von Karl Lashley. Das Problem ist, zu erklären, wie  serielle Ordnung in unserem Gehirn produziert und wahrgenommen werden kann. Denn das Gehirn ist netzwerkartig organisiert und macht sehr viele Dinge parallel. Ein Beispiel ist das vor einigen Jahren als Typoglycemia bekannt gewordenen Phänomen, dass es laut enier Sduite an enier Elingshcen Unvirestiät (...) eagl sei, in welcher Reihenfolge Buchstaben innerhalb von Wörtern angeordnet seien. Obschon diese Behauptung nur mit Einschränkungen gilt, zeigt das Phänomen dennoch, dass Reihenfolgen, die in der Umwelt existieren, vom Gehirn teilweise parallelisiert werden. Nur darum sind wir in vielen Anforderungen um ein Vielfaches besser als Computer, obwohl die Geschwindigkeit, mit der unsere Nerven Impulse weitergeben, im Vergleich zu Schaltvorgängen in Computern sehr niedrig ist. Während die Hirnforschung zum Beispiel Oszillationen um 40 Hz mit dem Verknüpfen von Sinneseindrücken in Verbindung bringt, schalten handelsübliche Computer bei zum Beispiel drei Milliarden Hz. Allerdings können viele Millionen Nervenzellen gleichzeitig Impulse senden, während handelsübliche Computer nur einen bis acht Prozesse parallel ausführen.

Drängeln an der Bar – Drängeln im Gehirn

Computern das parallele Rechnen beizubringen, verlangt viel Überlegung. Gut, dass wir uns nicht erst entsprechende Gedanken machen müssen, damit unser Gehirn es schafft, verschiedene Operationen gleichzeitig durchzuführen. Unser Gehirn kann das schon. Gerade diese Parallelität aber stellt uns vor die spannende Frage, wie es das Gehirn schafft, Reihenfolgen sowohl präzise als solche wahrzunehmen als auch zu produzieren. Dabei mag es erstaunen, dass eine der besonders erfolgreichen und eleganten Lösungen des Gehirns für das Reihenfolge-Problem eher mit dem chaotischen Gedränge in einer vollen Bar zu vergleichen ist, als wohlmöglich mit dem systematisch geordneten Vorgehen in einem Labor. Möglicherweise ist es im Forschungsalltag produktiv, auf manche Ablenkung nicht ganz zu verzichten. Wenn beispielsweise vier Wissenschaftler/innen auf den Tag im Labor eine Stunde in einer Bar folgen lassen, könnten sie eine erstaunliche Beobachtung machen. Die Vier mögen gleichzeitig versuchen, Kopf und Arme durch die Menschenmenge in  Richtung Theke zu schieben, sich weit in Richtung Bartender zu biegen, den Mund aufzureißen und mit den Armen zu wedeln – bedient werden können sie dennoch nicht gleichzeitig, sondern eine/r nach dem anderen, da ja nur eine Bedienung vorhanden ist. Trotz parallelen Ansturms auf die Bar wird also sequentiell abgefertigt bzw. abgefüllt. Die Reihenfolge ist dabei keineswegs zufällig: Die Person, die am lautesten schreit und am besten drängelt, wird zuerst bedient. Sobald sie ein Getränk in der Hand und den Mund voll hat, ist sie nicht mehr die lauteste Person, sondern die Person, die bisher am zweitlautesten war, ist nun in der besten Position, die Aufmerksamkeit des Bartenders zu erlangen. Wenn sie ihr Getränk hat, kommt die dritte Person zum Zuge bzw. zu einem Getränk usw. Trotz gleichzeitigen Ansturms auf die Bar gibt es also eine serielle Struktur. Beim nächsten Besuch wird wieder in der gleichen Abfolge bedient – wenn sich nichts an den Fähigkeiten der Vier ändert, Aufmerksamkeit zu gewinnen. Wenn alle wie gewohnt drängeln, dann stellt sich also die gewohnte Reihenfolge ein – drängeln ist gut für die Reihenfolge.

Abbildung 1: Reihenfolge durch Drängeln. Foto: Jörg Nicht, 2014, www.joergnicht.comAnalog zu dieser Bar-Geschichte können Competitive Queuing Modelle erklären, wie das Gehirn Reihenfolgen produziert (Bullock, 2004; Houghton & Hartley, 1995). Da steckt die Idee vom Drängeln also mit drin. Die Elemente einer zu produzierenden Reihenfolge sind alle gleichzeitig aktiv – aber unterschiedlich stark. Das stärkste Element kommt zuerst dran und wird dann gehemmt. Dadurch kommt dann das zweitstärkste zum Zuge usw. Dass die Elemente kurzer Sequenzen alle schon präsent sind, bevor sie eines nach dem anderen abgearbeitet werden, wissen wir unter anderem aus der Analyse von Tippfehlern. Da kommen oft Buchstaben vor, die eigentlich erst spätre dran wären – und wenn sie dann dran wären, werden sie nicht wiederholt.

Affen am Automaten

Wenn Reihenfolge, wie eben geschildert, ausschließlich durch die Stärke der Elemente der Reihenfolge bestimmt werden würde, dann hätten wir immer dann ein Problem, wenn sich ein Element wiederholen soll – wie beispielsweise das e in Element. Wenn sich e an der Bar zuerst vordrängelt und bedient wird, wie kann e es schaffen, kurz darauf wieder bedient zu werden, obwohl es sich eigentlich wieder hinten anstellen müsste? Gäbe es für e nur einen (Drängel)Stärke-Wert, wäre es also nicht ohne Weiteres möglich zu kodieren, wann es wieder und wieder dran kommen soll.

Hier kommen die Affen ins Spiel, denn Aufschluss über diese Frage haben uns Beobachtungen an unseren nahen Verwandten ermöglicht, obschon diese ja nicht sprechen können und sich keine Gedanken über wiederkehrende Buchstaben machen müssten. Die Versuche liefen folgendermaßen ab (Terrace, 2005): Die Affen können auf Karten tippen, von denen mehrere gleichzeitig auf dem Bildschirm zu sehen sind. Wenn die Felder in einer vorher festgelegten Reihenfolge angetippt werden, dann gibt es eine Belohnung. Die Teilnahme an dem Reihenfolge-Rätsel ist freiwillig, ausreichend Futter gäbe es auch für Touchscreen-Muffel. Allerdings arbeiten die Tiere recht kontinuierlich daran, die Reihenfolgen zu lernen, die zu verschiedenen Kartensätzen gehören. Wie also schaffen es die Tiere, die Karten in der richtigen Reihenfolge zu drücken, obwohl alle Karten immer gleichzeitig auf dem Bildschirm präsentiert werden? Einerseits könnten sie wissen, dass gerade Karte C dran ist, weil sie eben Karte B (und kurz davor  Karte A) gedrückt haben. Andererseits können sie auch wissen, dass Karte C dran ist, weil sie „mitgezählt“ haben: Sie wissen, dass sie schon zwei Karten gedrückt haben, nun also die dritte Karte dran ist und diese Karte immer C ist. Das gleiche gilt für uns Menschen: Wenn wir an einem Geldautomaten unsere PIN eintippen um Bargeld abzuheben, dann können wir beispielsweise als dritte Nummer die „5“ entweder deshalb drücken, weil wir davor die „7“ getippt haben und in unserer PIN die „7“ mit der darauffolgenden „5“ verknüpft ist. Unbewusstes Wissen dieser Art hat Herrmann Ebbinghaus schon 1885 nachgewiesen. Alternativ drücken wir die „5“, weil wir wissen, dass die dritte Nummer die „5“ ist. In solch einem Fall würden wir an dritter Stelle selbst dann die „5“ eintippen, wenn wir uns zuvor geirrt und an zweiter Stelle die „2“ statt der „7“ getippt hätten. Diese Form von Wissen haben unter anderem Schimpansen unter Beweis gestellt. Ein beliebter Name für Schimpansen im Labor ist übrigens Ebbinghaus. Die Unterscheidung zwischen den beiden Reihenfolge-Wissensformen ist interessant. Die erste Möglichkeit (Wissen, dass auf „A“ dann „B“ folgt; auch als „Chaining“ bezeichnet) kann das Problem der Wiederholung desselben Elements nicht lösen, ohne zu weiteren Problemen zu führen. Es bliebe in Element unklar, wann auf das „e“ ein „l“ oder ein „m“ oder ein „n“ folgen sollte. Wenn unser Gehirn die zusätzliche Information darüber hat, an welcher Position der Reihenfolge man gerade ist, dann kann es dafür sorgen, dass beispielsweise, das „e“ in Element an dritter und fünfter Position eine erneute, zusätzliche Aktivierung (Drängel-Stärke) bekommt, obwohl es ja eigentlich bereits an erster Position bedient wurde.

Zurück zu den Affen! Nach Übung mit verschiedenen Reihenfolgen ist deutlich, dass die Affen die Reihenfolgen von Karten gespeichert haben. Sie können beispielsweise vier verschiedene jeweils aus vier Karten bestehende Reihenfolgen korrekt drücken. Wenn z.B. auf dem Bildschirm die vier Symbol-Karten Vogel, Blume, Frosch und Muschel mit zufälliger Platzierung gezeigt werden, tippen die Affen die Reihenfolge Vogel, Blume, Frosch und Muschel. Gleiches gilt, wenn  Baum, Fisch, Frosch und Person gezeigt werden, usw. Es bedarf jedoch eines geschickten Tests um herauszufinden, wie sie die Folgen gespeichert haben (vgl. Chen, Swartz, & Terrace, 1997). Dafür werden die Viererpäckchen aus der Lernphase durchmischt. Es werden nun vier Karten zusammen auf dem Bildschirm angeboten, die in der Lernphase nicht gemeinsam vorkamen. Jedoch kam eine Karte (in ihrem Vierer-Päckchen) als erste Karte dran, eine andere  als zweite, eine weitere als dritte und schließlich eine als vierte Karte. Tastsächlich drücken die Affen die ehemals erste Karte zuerst, usw. Sie haben also beim Erlernen der Reihenfolgen mit abgespeichert, welche Karte als erste, zweite, dritte und vierte angetippt wird. Sie haben sich nicht darauf verlassen, welche Karte nach welcher spezifischen anderen Karte gedrückt wird (also beispielsweise Blume nach Vogel).

Wenn (wie bei Affen) solches Reihenfolgen-Lernen und -Nutzen ohne Sprache möglich ist, dann ist es vielleicht sogar unbewusst und unabsichtlich möglich. Aus einer Reihe ähnlich aufgebauter Experimente zum impliziten Sequenzlernen (Gaschler, 2013) wissen wir tatsächlich, dass Menschen auch unabsichtlich und unbewusst (also ohne absichtliches „Mitzählen“) solche Reihenfolge-Information lernen  (Schuck, Gaschler, Keisler & Frensch, 2012). Sie lernen beiläufig und ohne das Bewusstsein, dass es etwas zu lernen gäbe, und wissen gar nicht, dass sie Reihenfolgen gelernt haben. Man kann zudem mehrere Arten der Reihenfolgenspeicherung parallel nutzen und so oft schneller zu einem stabileren Ergebnis kommen (Schuck, Gaschler & Frensch, 2012).

Zu viel oder zu wenig Reihenfolge

Wie bereits am Beispiel der Rechtschreibfehler eingeführt, macht sich die Bedeutung eines oder mehrerer Mechanismen der Reihenfolgeproduktion besonders bemerkbar, wenn diese nicht (mehr) hinreichend funktionieren. Dabei kann es vorkommen, dass Reihenfolgen nicht flüssig produziert werden können, wie es zum Beispiel beim Stottern oder einer Lese-Rechtschreib-Schwäche (Jiménez-Fernández, Vaquero, Jiménez & Defior, 2011) der Fall sein kann. Andererseits kann es auch vorkommen, dass Reihenfolgen gar nicht mehr richtig als solche vom Gehirn aufgenommen werden können. Aus Experimenten in der Hirnforschung wissen wir, dass subkortikale Strukturen, insbesondere das Striatum, für die Speicherung und den Abruf motorischer Sequenzen wichtig sind. Da diese Struktur während des Alterungsprozesses beeinträchtig wird (Schuck, Frensch, Schjeide, Schroeder, Bertram & Li, 2013) oder im Rahmen einer Erkrankung, wie der Parkinson-Krankheit (Ferraro, Balota & Connor, 1993) stark geschädigt werden kann, kann es hier zu Problemen beim Neuerwerb oder dem Abruf von (motorischem) Sequenzwissen kommen.

Andererseits ist es auch möglich, dass wir zu stark an Reihenfolgen festhalten, obwohl eine flexiblere Strategie von Nutzen wäre. Dies lässt sich in besonderem Maße bei Patient/innen mit einer Zwangsstörung beobachten – bei welcher mitunter ebenfalls das Striatum in seiner Funktion geschädigt ist (Kathmann, Rupertseder, Hauke & Zaudig, 2005).

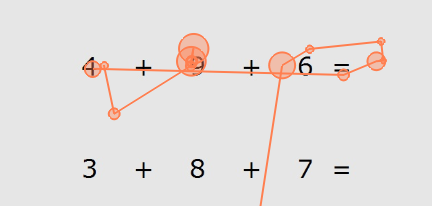© Robert GaschlerAuch beim Lösen einfacherer Kopfrechenaufgaben kann ein starres Festhalten an Reihenfolgen zu Problemen führen. Effizientes Kopfrechnen in der Grundschule und darüber hinaus kann beispielsweise erfordern, dass man flexibel die Reihenfolge von Summanden oder Faktoren anpasst. Bei 4 + 9 + 6 könnte man zunächst 4 + 6 berechnen, um den Vorteil der Zehner-Addition zu nutzen (Abbildung 2). Ein weiteres Beispiel: Wenn man gerade 8 + 5 + 3 berechnet hat und danach 5 + 3 + 8 lösen soll, könnte man sich nochmaliges Rechnen sparen, wenn man die Anordnung der Summanden flexibel betrachtet. Einerseits können Kinder bereits am Anfang der Grundschule Reihenfolgen flexibel nutzen, wenn sie darauf hingewiesen werden, dass dies für schnelles Rechnen förderlich sei. Andererseits fällt es sowohl Grundschulkindern als auch Erwachsenen oft erstaunlich schwer, spontan – also ohne Hinweis – Vereinfachungsmöglichkeiten zu erkennen und zu nutzen, die einen flexiblen Umgang mit Rechenreihenfolgen erfordern (Gaschler, Vaterrodt, Frensch, Eichler & Haider, 2013).

Zusammenfassung

Wir können mit experimentellen Methoden herausfinden, wie unser Gehirn – obwohl es überwiegend parallel arbeitet – hochgradige Präzision beim Wahrnehmen, Speichern und Abarbeiten von Reihenfolgen erreichen kann. Wir lernen Reihenfolgen absichtlich und unabsichtlich und wenden feste Reihenfolgen (z. B. von links nach rechts rechnen) oft unabsichtlich an.

Literatur

Bullock, D. (2004). Adaptive neural models of queuing and timing in fluent action. Trends in Cognitive Sciences, 8, 426-433.
Chen, S., Swartz, K. B., & Terrace, H. S. (1997) Knowledge of the ordinal position of list items in rhesus monkeys. Psychological Science, 8, 80–86.
Ebbinghaus, H. (1885/1913). Über das Gedächtnis [Memory: A contribution to experimental psychology] (Henry A. Ruger & Clara E. Bussenius, Trans.). Retrieved from http://psychclassics.yorku.ca/Ebbinghaus/index.htm (Original work published 1885)
Ferraro, F. R., Balota, D. A. & Connor, L. T. (1993). Implicit memory and the formation of new associations in nondemented Parkinson's disease individuals and individuals with senile dementia of the Alzheimer type: A serial reaction time (SRT) investigation. Brain and Cognition, 21, 163-180.
Gaschler, R. (2013). Implizites Lernen. In M. A. Wirtz (Hrsg.), Dorsch – Lexikon der Psychologie. Abgerufen am 30.01.2014, von https://portal.hogrefe.com/dorsch/implizites-lernen/
Gaschler, R., Vaterrodt, B., Frensch, P. A., Eichler A. & Haider, H. (2013). Spontaneous usage of different shortcuts based on the commutativity principle. PLoS ONE, 8(9): e74972. http://www.plosone.org/article/info%3Adoi%2F10.1371%2Fjournal.pone.0074972
Houghton, G. & Hartley, T. (1995). Parallel models of serial behavior: Lashley Revisited. Psyche, 2, 1-25.
Jiménez-Fernández, G., Vaquero, J. M., Jiménez, L. & Defior, S. (2011). Dyslexic children show deficits in implicit sequence learning, but not in explicit sequence learning or contextual cueing. Annals of Dyslexia, 61, 85-110.
Kathmann, N., Rupertseder, C., Hauke, W. & Zaudig, M. (2005). Implicit sequence learning in obsessive-compulsive disorder: Further support for the fronto-striatal dysfunction model. Biological Psychiatry, 58, 239-244.
Lashley, K. S. (1951). The problem of serial order in behavior. In L. A. Jeffress (Ed.), Cerebral mechanisms in behavior (pp. 112-136).  New York: Wiley.
Schuck, N. W., Frensch, P.A., Schjeide, B.-M., Schröder, J., Bertram, L. & Li, S.-C. (2013). Effects of aging and dopamine genotypes on the emergence of explicit memory during sequence learning. Neuropsychologia, 51, 2757-2769.
Schuck, N. W., Gaschler, R. & Frensch P. A. (2012). Implicit learning of what comes when and where within a sequence: The time-course of acquiring serial position- item and item- item associations to represent serial order. Advances in Cognitive Psychology, 8, 83-97. http://www.ac-psych.org/download.php?id=114
Schuck, N. W., Gaschler, R., Keisler, A. & Frensch P. A. (2012). Position–item associations play a role in the acquisition of order knowledge in an implicit serial reaction time task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 38, 440-456.
Terrace, H. S. (2005). The simultaneous chain: A new approach to serial learning. Trends in Cognitive Sciences, 9, 202-210.