Ausgabe 3 2014 / Medienpsychologie

Neue Medien, neue Möglichkeiten: Wie Lernsoftware mathematisches Wissen vermittelt

• von Ursula Fischer, Tanja Link, Hans-Christoph Nürk, Ulrike Cress & Korbinian Möller

In unserem digitalen Zeitalter sind Smartphones, Tablets und Notebooks aus dem Alltag nicht mehr wegzudenken. Entsprechend wächst das Angebot an Lernsoftware und multimedialen Lernspielen. Wie sinnvoll diese Spiele sind und ob man tatsächlich dauerhaft etwas damit lernt, lässt sich für unbedarfte Nutzer/innen aber oft nicht erkennen. Abhilfe sollen wissenschaftlich fundierte Trainingsprogramme schaffen, die vor ihrer Markteinführung auf ihre Wirksamkeit hin untersucht werden. Die rasante Entwicklung neuer Technologien hat hier stetig neue Möglichkeiten für motivierende und wirksame Lernspiele eröffnet.

Einleitung

Die Zeit auf meiner Mathematik-Trainings-App tickt. Ich habe 10 Sekunden, um den Durchschnitt aus 37, 48, 25 und 18 zu berechnen. Bei Ablauf der Zeit habe ich noch nicht einmal die vier Zahlen zusammenaddiert. Aber immerhin bin ich schon bis zur dritten Zahl gekommen, bevor mir die App verkündet, dass ich immer noch zu langsam bin. Wenn das so weitergeht, werde ich nie genug Sternchen für das nächste Level sammeln. Also ein neuer Versuch: Was ist der Durchschnitt aus 24, 40, 5 und 39?

Wenn jemand wie ich sich die Zeit mit Mathematik-Trainings vertreibt, dann geschieht dies meist aus ganz einfachen Gründen. Zum Beispiel, um die eigenen Fähigkeiten im Kopfrechnen wieder aufzufrischen. Besonders dann, wenn die Schulzeit schon länger zurückliegt und man sich selbst dabei erwischt hat, wie man 3+4 in den Rechner eintippt.

Eine große Auswahl an Apps macht dieses Auffrischen ganz einfach. Über 250 Treffer bekommt man allein für das Suchwort „Gehirntraining“ im Appstore eines Smartphones. Dasselbe gilt für „Mathematik Training“, und wahrscheinlich wären es noch mehr, läge das Limit der angezeigten Suchergebnisse nicht bei 250 Ergebnissen. Kurz gesagt, das Geschäft mit der Lernsoftware boomt.

Lernsoftware auf dem Vormarsch

Lernspiele, Apps, Gehirn Jogging™: Der Gedanke, durch ein paar tägliche Übungen die eigene Intelligenz erhöhen zu können, klingt ziemlich verlockend. Die größte Popularität haben Spiele zum Training der Denkleistung wie beispielsweise das Gehirn Jogging™ von Dr. Kawashima erreicht. Ein großer Teil der Aufgaben besteht dabei aus Mathematik – man soll Rechenaufgaben lösen, die Differenz zwischen zwei Uhrzeiten ermitteln, oder die Reihenfolge von Zahlen im Gedächtnis behalten.
Solche Denkleistungstrainings und Lernspiele sind ein Nebenprodukt unseres Zeitalters des sogenannten Ubiquitous Computing (englisch für „Rechnerallgegenwart“ oder auch die Allgegenwärtigkeit der rechnergestützten Informationsverarbeitung/EDV). Damit ist gemeint, dass zum Beispiel Smartphones und Tablets, aber auch Handheld-Spielekonsolen (wie z. B. Nintendo 3DS™) dafür gesorgt haben, dass wir immer und jederzeit lernen können. Es ist dabei komplett uns selbst überlassen, was wir wo und wann lernen.

Aber welchen Nutzen bringen diese Spiele wirklich? Nehmen wir zum Beispiel das äußerst erfolgreiche Gehirn Jogging™ von Dr. Kawashima. Es existieren sowohl Studien, die wissenschaftlich eine breite Wirkung nachgewiesen haben (z. B. Schmiedek, Lövdén & Lindenberger, 2010), als auch Studien, die ausschließlich Verbesserungen in den trainierten Aufgaben fanden, aber keinen Transfer auf andere kognitive Leistungen (z. B. Owen et al., 2010).
Welche Ursache könnte es haben, dass diese Spiele sich teilweise als nicht wirksam herausstellen? Eine Möglichkeit könnte sein, dass zum Beispiel Gehirn Jogging™ und auch der Nachfolger Gehirntraining™ zwar sehr viele verschiedene Aufgaben trainieren, diese aber nicht besonders tiefgehend.

Eine weitere denkbare Ursache könnte sein, dass die meisten Lernspiele und Apps sehr anspruchsvolle Aufgaben enthalten. Interessanter ist dagegen ein Blick auf Lernsoftware, die darauf abzielt, Schwächen im Basisbereich auszugleichen, indem einfachere Aufgaben geübt werden. Vor allem im Bereich der Mathematik sind solche Lernansätze gefragt, da mathematische Kompetenzen großteils hierarchisch aufeinander aufbauen. So hat sich gezeigt, dass Trainings im mathematischen Basisbereich einen größeren Lerneffekt bewirken als Trainings komplexer mathematischer Fähigkeiten (siehe Kroesbergen & van Luit, 2003, für eine Metaanalyse).

Relevanz mathematischer und numerischer Fähigkeiten

Es gibt einen einfachen Grund dafür, warum Lernsoftware für Mathematik so relevant ist: Mathematische und numerische Fähigkeiten gewinnen für unseren Alltag immer mehr an Bedeutung. Aktuelle Studien besagen beispielsweise, dass unzureichende numerische Fähigkeiten im Alltags- und Berufsleben inzwischen schlechter zu kompensieren sind als unzureichende Lese- und Rechtschreibfähigkeiten (Parsons & Bynner, 2005). Außerdem zeigt sich, dass Schüler(innen mit stark unterdurchschnittlichen mathematischen Leistungen überdurchschnittlich häufig schulische Sonderförderung in Anspruch nehmen, die Schule schwänzen oder auch vom Unterricht ausgeschlossen werden (Gross, Hudson, & Price, 2009).

Die Probleme in Mathematik beziehen sich dabei jedoch nicht auf höhere Mathematik, wie zum Beispiel Algebra, sondern auf grundlegende Zahlenverarbeitungs- und Rechenfertigkeiten. Dazu gehören zum Beispiel (i) fehlerfreies Zählen bis 20, (ii) Lesen, Schreiben, Ordnen und Vergleichen von Zahlen im Raum bis 100, (iii) Addition und Subtraktion zweistelliger Zahlen, (iv) Benutzen und Interpretieren Können von Rechenzeichen, (v) Rechnen in ganzen Einheiten (z. B. EUR) und (vi) Lesen und Angeben der Uhrzeit. Diese Fähigkeiten entsprechen weitgehend dem Curriculum der zweiten und dritten Klasse an deutschen Grundschulen. Erwirbt ein Kind diese Fähigkeiten nicht, ist es nicht verwunderlich, dass das tägliche Leben dadurch beeinträchtigt wird.
Besonders Kinder mit Schwierigkeiten in Mathematik brauchen daher eine frühe und dem aktuellen Leistungsstand entsprechende Förderung. Hier kann die Entwicklung neuer Lernsoftware Unterstützung bieten. Da die Probleme oft schon im Basisbereich der Mathematik beginnen, ist wichtig, dass die Förderung auch dort ansetzt. Verbessert man die Basisfertigkeiten, ist häufig auch ein Transfereffekt auf andere mathematische Kompetenzen zu beobachten (Kroesbergen & van Luit, 2003). Unter Transfer versteht man dabei einen Effekt des Trainings auf nicht gezielt trainierte Bereiche. So kann zum Beispiel ein Training der richtigen Reihenfolge von Zahlen durch ein Brettspiel dazu führen, dass Kindergartenkinder ein Verständnis für das Prinzip der Addition entwickeln und Additionsaufgaben besser lösen können (z. B. Ramani & Siegler, 2011).

Spannend ist im Bereich der Mathematik die Entwicklung neuer Lernsoftware zu beobachten, die durch den Einsatz neuer Medien einen größeren Lernzuwachs verspricht. Lern- und Übungsprogramme für den PC, insbesondere für Grundschüler/innen, gibt es schon lange. Oft handelt es sich bei solchen Software-Angeboten allerdings um Ergänzungen zu Lehrbüchern, die nicht gezielt auf die Schwächen einzelner Kinder eingehen und auf einem zu hohen Niveau ansetzen. Die Anzahl von wissenschaftlich evaluierten Lernprogrammen und -spielen für unterschiedliche Medien nimmt jedoch zu, und diese bauen immer häufiger auf aktuellen pädagogischen und psychologischen Erkenntnissen auf.

Als wissenschaftlich evaluiert wird ein Lernprogramm in der psychologischen und auch pädagogischen Forschung dann bezeichnet, wenn es sich in einer Studie mit Prä-Post-Vergleich als wirksam herausgestellt hat. Dabei wird zunächst der Leistungsstand einer Stichprobe von Kindern vor dem Training erhoben. Dann werden die Kinder in Gruppen eingeteilt: Eine Gruppe (die sogenannte Experimentalgruppe) erhält das Training, das auf seine Wirksamkeit untersucht werden soll. Eine zweite Gruppe (die Kontrollgruppe) erhält für gewöhnlich ein anderes Training, gegen das sich das evaluierte Training behaupten soll. Nach Abschluss des Trainings wird erneut die Leistung der Kinder gemessen und so die Verbesserung im Vergleich zur Ausgangsleistung bestimmt. Nur wenn das Experimentaltraining zu gleich großen oder sogar größeren Verbesserungen führt als das Kontrolltraining, wird es als wirksam beurteilt.

Lernsoftware für den mathematischen Basisbereich

Lernsoftware wurde besonders für junge Kinder als lernförderlich nachgewiesen (Li & Ma, 2010). Dafür verantwortlich ist unter anderem die Möglichkeit adaptiver Lernsoftware, bei der das Programm die Schwierigkeit der Aufgaben gezielt an die Leistung des Kindes anpassen kann. So durchläuft ein Kind nicht eine fix vorgegebene Reihe von Aufgaben, sondern erhält je nach Leistung in einer Aufgabe als nächstes eine schwierigere oder leichtere Aufgabe. Da schwache Kinder so nicht überfordert werden, erhöhen adaptive Spiele auch die Motivation und steigern besonders die Leistung schwacher Kinder.

Im englischen Sprachraum existieren schon länger mehrere Computerprogramme zur Förderung numerischer und rechnerischer Kompetenzen. Beispiele für solche Programme sind das „Number Race“ (ältere Versionen auch auf Deutsch; http://www.thenumberrace.com/nr/nr_download.php?lang=en) sowie der „Number Catcher“ für älter Kinder (http://www.thenumbercatcher.com/nc/home.php?lang=en) und das umfangreiche Angebot der „Building Blocks Software“ (https://www.mheonline.com/program/view/4/4/406/0076189031/). Im deutschen Sprachraum wurden in jüngeren Jahren die „Rechenspiele mit Elfe und Mathis I und II“ (http://www.hogrefe.de/programm/rechenspiele-mit-elfe-und-mathis-i.html) und das Programm „Dybuster® Calcularis“ (http://www.calcularis.ch/de/) entwickelt. Mit der Etablierung dieser Programme haben PC-basierte Lernspiele Einzug in die Lerntherapie und Nachhilfe gehalten.

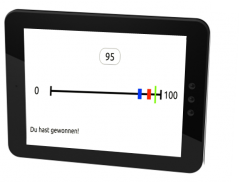Bild: Ursula FischerDie Forschung am Institut für Wissensmedien in Tübingen hat sich ebenfalls mit computergestützten Trainings für Mathematik und der Förderung mathematischer Basiskompetenzen beschäftigt. Zum Beispiel wird dort zurzeit eine Lernplattform entwickelt, auf die nach der Fertigstellung online jederzeit von überall zugegriffen werden kann (vorläufige Testversion auf http://lernplattform.iwm-kmrc.de/). Unter anderem wurden bereits interaktive Browserspiele zum Multiplizieren und zum Einschätzen von Zahlen auf einem Zahlenstrahl entwickelt. Die Spieler/innen können dabei von unterschiedlichen Orten aus gegeneinander spielen und sollen dabei so schnell wie möglich antworten, bevor ihr Gegner/innen ihnen zuvorkommt. Dadurch verbessert sich die Lösungsgeschwindigkeit der Kinder, und die Verwendung zeitraubender Strategien, wie zum Beispiel zählendes Rechnen, wird vermieden.

Interessant sind in diesem Kontext auch andere mediengestützte Ansätze, die noch nicht kommerziell vertrieben werden. Dazu zählen zum Beispiel Ansätze, die sich die körperliche Erfahrung numerischer Konzepte zum Ziel gemacht haben. Hier spielen neue Entwicklungen im Bereich interaktiver Medien eine entscheidende Rolle.

Lernspiele mit Bewegungskomponente

Einen ganz neuen Ansatz für Lernsoftware bieten Lernspiele unter Einbezug körperlicher Bewegung. Die theoretische Basis dafür bietet die Theorie der sogenannten Embodied Cognition (~ verkörperlichte Kognition), die davon ausgeht, dass Denkprozesse und kognitive Vorgänge immer in Wechselwirkung mit körperlichen Wahrnehmungen und Handlungen stattfinden (z.B. Barsalou, 2008). Neue digitale Lernspiele nutzen solche körperlichen Erfahrungen gezielt, um numerische Kompetenzen zu fördern. Der entscheidende Faktor für den Erfolg solcher Trainings liegt dabei darin, dass Eigenschaften von Zahlen mit dem ganzen Körper erfahren werden können. Dafür eignen sich besonders räumliche Eigenschaften von Zahlen wie zum Beispiel die Distanzen zwischen Zahlen auf einem Zahlenstrahl oder die Verknüpfung von kleinen Zahlen mit der linken und großen Zahlen mit der rechten Seite des Raumes.

Hierfür wurden neue Entwicklungen in der Welt der digitalen Spielemedien gezielt für numerische Trainings eingesetzt. Es gibt mittlerweile verschiedenste bewegungsgesteuerte Eingabemedien für verschiedene Spielekonsolen, die Benutzerbewegungen und Gesten erfassen können. Diese sind für Lernzwecke besonders geeignet, da sie ein tieferes Eintauchen der Spieler/innen in den Spielinhalt fördern und damit auch Motivation und Aufmerksamkeit aufrechterhalten (Bianchi-Berthouze, Kim, & Patel, 2007).

Bild: Ursula FischerUnter anderem wurde eine digitale Tanzmatte für die Entwicklung unterschiedlicher Lernspiele verwendet. Ursprünglich erschien diese als Zubehör zu verschiedenen Spielekonsolen wie der PlayStation™, nun ist sie aber auch für PCs erhältlich und ermöglicht mit 3x3 Feldern verschiedene Eingabeformate. So sollten Kindergartenkinder in einem Lernspiel für die Entscheidung, ob eine Zahl größer oder kleiner ist als eine andere, entweder auf das rechte (größer) oder linke (kleiner) Feld der Tanzmatte springen (Fischer, Moeller, Bientzle, Cress & Nuerk, 2011). Diese Aufgabe klingt trivial – für Kindergartenkinder ist sie aber nicht nur eine Herausforderung, sondern auch eine Voraussetzung für spätere mathematische Kompetenzen. Die Kindergartenkinder verbesserten sich durch das Spiel nicht nur darin, Zahlen auf einem Zahlenstrahl anzuordnen, sondern auch in ihren Zählfertigkeiten (z. B. dem Zählen in Zweierschritten oder dem Rückwärtszählen von 10).

Die Idee solcher körperlicher Trainings wurde mittlerweile auch weiterentwickelt, indem mithilfe des Kinect–Sensors der XBox 360™ die Bewegung von Kindern erfasst wurde (Link, Moeller, Huber, Fischer & Nuerk, 2013). Der Kinect-Sensor besteht aus einer Kamera mit Infrarotsensor, die die Position eines Menschen im Raum über eine Ausdehnung von bis etwa 3,5 m Breite bestimmen und aufzeichnen kann. Erstklässler/innen bewegten sich dabei auf einem auf den Boden geklebten Zahlenstrahl um die geschätzte Position einer Zahl anzugeben. Durch dieses Lernspiel verbesserten sich die Kinder nicht nur in der Einschätzung von Zahlen auf einem Zahlenstrahl, sondern auch in Additionsaufgaben, was erneut einem Transfereffekt auf eine komplexere Aufgabe entspricht (siehe auch Fischer & Moeller, 2014).

Die Zukunft der Lernsoftware

Brain Studies via freedigitalphotos.net (http://www.freedigitalphotos.net/images/Education_g314-Brain_Studies_p22348.html), terms of use (http://www.freedigitalphotos.net/images/terms.php)Solche und andere Studien zeigen, dass Lernsoftware nicht nur in Form von Computerspielen wirksam sein kann. Kinder mit Schwierigkeiten in Mathematik, aber auch Kinder mit geringeren kognitiven Fähigkeiten können beim Lernen davon profitieren, wenn zusätzlich zum Unterricht wissenschaftlich evaluierte Lernspiele eingesetzt werden (siehe z. B. Ramani & Siegler, 2011). Eine integrierte Bewegungskomponente kann einen zusätzlichen Bonus darstellen – nicht nur, weil sie motiviert und weniger langweilig ist als bloßes Herumsitzen vor dem Computer, sondern auch, weil Bewegung selbst helfen kann, Zusammenhänge zu verstehen, wenn sie einen direkten Bezug zur Lernaufgabe hat. Zum Beispiel kann die Verknüpfung zwischen Zahlen und Raum gezielt durch Bewegung entlang eines Zahlenstrahls gestärkt werden.

Egal, ob ein Erwachsener damit versucht, vergessenes Schulwissen wieder aufzufrischen oder ein Kind mathematische Konzepte zu verstehen lernt: Lernsoftware für Mathematik entwickelt sich rasant weiter und gewinnt für die Wissensvermittlung auch außerhalb des Mathematikunterrichts stetig an Bedeutung.

 

Referenzen

Barsalou, L. W. (2008). Grounded cognition. Annual Review of Psychology, 59, 617–45. doi:10.1146/annurev.psych.59.103006.093639

Bianchi-Berthouze, N., Kim, W. & Patel, D. (2007). Does body movement engage you more in digital game play? And why? In Affective Computing and Intelligent Interaction (pp. 102-113).

Fischer, U. & Moeller, K. (2014). Aktuelle Befunde zu Zahlenstrahltrainings - Verschiedene Ansätze und deren Wirksamkeit. In G. Schulte-Körne (Ed.), Legasthenie und Dyskalkulie: Neue Methoden zur Diagnostik und Förderung (pp. 33–50). Bochum: Verlag Dr. Dieter Winkler.

Fischer, U., Moeller, K., Bientzle, M., Cress, U. & Nuerk, H.-C. (2011). Sensori-motor spatial training of number magnitude representation. Psychonomic Bulletin & Review, 18, 177-183. doi:10.3758/s13423-010-0031-3

Gross, J., Hudson, C. & Price, D. (2009). The long term costs of numeracy difficulties. London: Every Child a Chance Trust and KPMG.

Kroesbergen, E. H. & van Luit, J. E. H. H. (2003). Mathematics interventions for children with special educational needs: A meta-analysis. Remedial and Special Education, 24, 97–114. doi:10.1177/07419325030240020501

Li, Q. & Ma, X. (2010). A meta-analysis of the effects of computer technology on school students’ mathematics learning. Educational Psychology Review, 22, 215–243. doi:10.1007/s10648-010-9125-8

Link, T., Moeller, K., Huber, S., Fischer, U. & Nuerk, H.-C. (2013). Walk the number line – An embodied training of numerical concepts. Trends in Neuroscience and Education, 2, 74–84.

Owen, A. M., Hampshire, A., Grahn, J., Stenton, R., Dajani, S., Burns, A. S., … Ballard, C. G. (2010). Putting brain training to the test. Nature, 465(7299), 775–778. doi:10.1038/nature09042

Parsons, S. & Bynner, J. (2005). Does Numeracy Matter More? London: National Research and Development Centre for Adult Literacy and Numeracy.

Ramani, G. B. & Siegler, R. S. (2011). Reducing the gap in numerical knowledge between low-and middle-income preschoolers. Journal of Applied Developmental Psychology, 32, 146–159. doi:10.1016/j.appdev.2011.02.005

Schmiedek, F., Lövdén, M. & Lindenberger, U. (2010). Hundred says of cognitive training enhance broad cognitive abilities in adulthood: Findings from the COGITO study. Frontiers in Aging Neuroscience, 2(July), 1–10. doi:10.3389/fnagi.2010.00027